Problema sobre um jogador que não pode ser expulso do casino

No âmbito do projeto especial de colaboração com a Corretora Prime EXANTE o Insider.pro continua a série de artigos de divulgação científica "Matemática do Infinito e a Realidade das Finanças" do doutorado em Física e Matemática Viktor Argonov sobre os paradoxos da teoria dos jogos e da sua aplicação a assuntos financeiros.

O problema sobre o passeio do bêbado perto do bar que discutimos no artigo "Traders e bêbedos" é um problema divertido e conveniente para apresentar a unidade abstrata, tal como o passeio aleatório de um ponto pela linha reta. Mas o movimento dos bêbados preocupa as pessoas muito menos que o movimento dos capitais. Por exemplo, ainda nos anos 1650 os cientistas Blaise Pascal e Christiaan Huygens começaram a estudar o assim chamado problema da falência de um jogador. O problema tem várias formulações, mas vamos focar-nos numa delas — especialmente paradoxal.

Um jogador compra no casino M fichas, cada uma das quais custa $1 (o dinheiro pago pelas fichas é o seu pagamento pela participação no jogo). A cada minuto o croupier atira uma moeda. Quando cai cara - tira uma das fichas ao jogador. Quando cai coroa - dá, ao jogador, uma ficha adicional. O número de fichas do casino não é restrito, logo o casino não pode falir - ao contrário do jogador. O jogo continua até o jogador perder todas as fichas. Deste modo, não irá ganhar dinheiro. O jogo é "unilateral" mas enquanto continua o jogador tem direito a comer, beber, comunicar com outros jogadores e divertir-se de vários modos por conta do casino (não é necessário estar ao lado do croupier, que faz tudo honestamente).

Colocamos, então, quatro questões:

Este problema quase coincide com o problema dos bêbados. O atirar de moeda é igual a um passo. O aumento ou diminuição do número de fichas é parecido com o movimento para a frente e para trás. E a falência é igual à volta ao bar. Por isso, a probabilidade de falência do jogador cai à medida que o número N cresce pela mesma lei de potência, como a probabilidade de volta dos bêbados. Também haverá partidas de jogo prolongadas (voos de Lévy), devido às quais o tempo médio de falência do jogador é infinito. A única diferença é que o jogador não começa com zero fichas, mas antes com M. Por isso, o tempo mediano do jogo é diferente: é aproximadamente proporcional a M².

O que é que isto significa na prática?

Para começar, vamos considerar um caso muito simples: M=1. Um mendigo entra no casino com $1. Agora o problema aproxima-se do problema dos bêbados. O tempo mediano será de um passo (com a probabilidade de ½ de cair cara). Mas o tempo médio esperado do jogo, segundo as fórmulas, é igual à eternidade. Por que é perigoso para o casino?

Se ao casino não chegarem um nem dois mendigos mas antes 100, 1000 ou mais então quase metade dos mesmos poderá perder depois do primeiro passo, mas entre os restantes haverá sortudos que apresentam ao casino uma ameaça enorme. Assim, como no problema anterior havia uma percentagem de "aventureiros" que ia para longe do bar agora há uma parte de "sortudos" cujo jogo pode durar um dia, alguns meses ou anos (voos longos de Lévy).

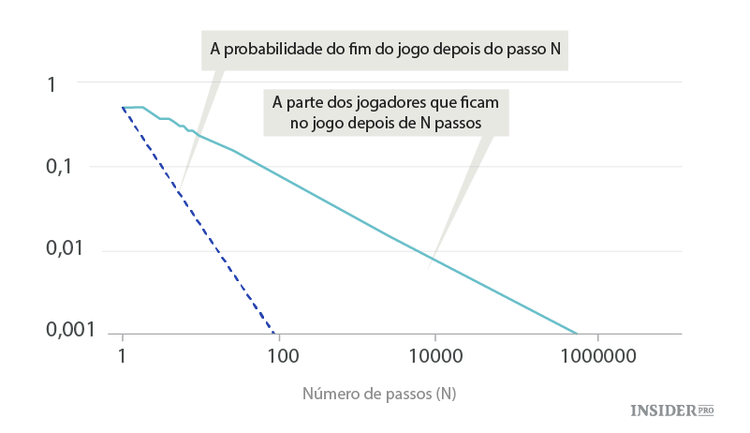
O número de "sortudos" será quase igual ao número de "aventureiros" no problema dos bêbados. Basta olhar para os gráficos. À medida que aumenta o N, o número de jogadores que ficam no casino é inversamente proporcional à raiz de N. Um em cada dez jogadores ficará no jogo aproximadamente até ao centésimo passo, um em cada cem até ao décimo milésimo, e um cada mil até ao milionésimo!

Ou seja, se ao casino chegarem 1000 mendigos com $1, 1 ou 2 deles vão "residir" no casino por alguns anos! E se chegarem 10 mil mendigos um deles poderá obter o direito às diversões por centenas de anos! Isto tendo em conta que para a maioria dos outros participantes o jogo irá durar apenas alguns minutos.

Este problema mostra muito bem o quão prudentes deveriam ser os organizadores dos jogos de azar. Nem sempre os lucros e as perdas podem ser avaliadas aproximadamente. Enquanto o problema do passeio dos bêbados foi uma brincadeira, já no casino o jogo pode realmente decorrer desta forma, sem se desviar do modelo matemático. Parece que um problema simples em que todos os trunfos estão do lado do casino, pode, na verdade, levá-lo à falência.

Com o M>1, a situação para o casino pode ser ainda pior: agora os jogadores nem precisam de um grande número de jogadas.

O tempo mediano do jogo é igual a M². Ou seja, depende do capital inicial do jogador do mesmo modo que o tempo do jogo do mendigo mais sortudo depende do número de mendigos (e do seu capital total). Não é uma mera coincidência, há uma ligação profunda que vamos discutir abaixo. Mas para começar vamos avaliar previsões do jogo com várias M.

Se dois amigos forem ao casino e cada um apostar $10 um deles talvez possa divertir-se por conta do casino por mais de uma hora e meia (o tempo mediano do jogo é de 100 minutos). Se apostarem $100 cada um ambos terão grande probabilidade de se divertirem por lá durante um mês. 10 mil dólares é o suficiente para "residir" no casino por centenas de anos (!).

É fácil entender porque é que os resultados dos mendigos "sortudos" são tão parecidos aos dos indivíduos que inicialmente chegaram com muito dinheiro. Os sortudos são aqueles que em alguma fase do jogo conseguiram, devido a coroas aleotórias, construir um capital difícil de perder mais tarde. Quanto mais uma pessoa ganhou com coroas, mais difícil será fazé-la perder o dinheiro. Desproporcionalmente mais difícil.

Recordemos que no problema dos bêbados o desvio médio da trajetória do estado inicial é proporcional à raíz da sua duração. O bêbado que deu 100 passos provavelmente está a uns 10 passos do bar. E aquele que deu 10 mil passos - a 100 passos do bar. O contrário também está certo: se o bêbado está a 10 passos do bar terá de dar 100 passos para voltar ao bar (isto será o tempo mediano da sua volta). E se estiver a 100 passos — terá de fazer 10 mil passos. Do mesmo modo, se durante o jogo um mendigo conseguiu obter 9 coroas a mais que caras (e ganhar 10 fichas), o seu jogo adiante não será muito diferente do daquele que comprou 10 fichas ao início. Para os dois, o tempo mediano do jogo será de 100 minutos. Quem conseguiu obter 100 fichas poderá continuar o jogo por 10 mil minutos.

Esta conclusão da teoria dos jogos tem consequências de largo alcance: explica a desigualdade económica na sociedade e mostra o quão importante é ter uma "margem de segurança". Uma empresa ou uma pessoa rica que conseguiu obter um grande capital pode muitas vezes mantê-lo por séculos - enquanto startups pequenas aparecem e desaparecem com uma grande velocidade. Estes argumentos estão diretamente ligados à dinâmica das cotações das ações.