Teoria das cotações imprevisíveis

No âmbito do projeto especial em colaboração com a Corretora Prime EXANTE o Insider.pro continua a série de artigos de divulgação científica "Matemática do Infinito e a Realidade das Finanças" do doutorado em Física e Matemática Viktor Argonov sobre os parodoxos da teoria dos jogos e da sua aplicação a assuntos financeiros.

Os parodoxos com o passeio aleatório de uma pessoa bêbada que discutimos no artigo "Traders e bêbedos" e com o jogo no casino funcionam também com o mercado de ações - e muitas vezes de um modo inesperado, que leva os traders inexperientes à falência.

Muitos traders conhecem uma importante regra do jogo do mercado de ações: se você comprou uma ação que de seguida perdeu valor, não se apresse a vendê-la. É provável que mais cedo ou mais tarde esse valor volte à posição anterior ou chegue mesmo a crescer. É apenas uma questão de tempo. Muitas vezes um trader espera um mês, um ano, dez anos e a ação não recupera o preço. A empresa não parece estar falida, não há crise, mas a cotação não se restabelece e mantém-se quase no mesmo nível do preço de compra. Muda bastante, mas não recupera. Como se fosse de propósito. Na verdade, não há nenhum "propósito" mas sim mais um paradoxo da teoria dos jogos.

Vejamos o seguinte problema. Há várias ações no mercado com vários preços. Num só dia o preço de cada ação pode crescer ou diminuir $1 - a probabilidade é igual. O investidor entra na bolsa de valores uma vez por dia. No primeiro dia compra 1.000 unidades da primeira ação disponível - e espera que o preço da ação suba $1. Depois disso, vende todo o pacote de ações (ao receber o lucro de $1.000) e compra 1.000 unidades de outra ação. Espera que o preço suba $1, vende (novamente com lucro de $1.000) e assim por diante.

Vamos supor que nenhuma empresa pode falir - mesmo que o preço das ações seja negativo. Assim, o jogo para o investidor é um triunfo garantido: obterá lucro com cada acordo.

Colocamos duas questões:

Esta é uma nova forma de colocar o mesmo problema em relação ao passeio aleatório - e tempo do seu retorno ao valor inicial (mais precisamente — sobre a intersecção do valor inicial). E já sabemos o que podemos esperar.

Com uma probabilidade ½, o pacote pode ser revendido de forma rentável no dia seguinte; com uma probabilidade ⅛ — depois de três dias; etc. Para um em cada dez casos, aproximadamente, a espera será de 100 dias, para um em cada cem — 10 mil dias; em cada mil — 1 milhão de dias (3 mil anos). Com tempo ilimitado de jogo, o tempo médio de espera irá até ao infinito, e o lucro médio — ao zero.

Embora se trate de um problema idealizado, a formulação explica a razão pela qual a tática do jogo do mercado de ações não é solução para o enriquecimento ilimitado. Os traders sabem que esta situação é um jogo de ordem take-profit: vender uma ação assim que o preço exceder o preço da compra. É uma tática que é, com certeza, quase infalível (sem contar com as comissões), mas na sua forma pura não tem muita utilidade. Por isso vamos complicar um pouco o problema. Talvez algumas condições novas permitam tornar o jogo lucrativo?

As condições do problema permanecem as mesmas - mas vamos introduzir uma limitação adicional: se o preço das ações não subir $1 em X dias, o investidor vende-as - mesmo com perdas.

A limitação do tempo do ciclo de compra e venda "corta o nó górdio" de soluções eternas, mas ameaça com perdas. Terá mais lucros ou perdas?

Vamos supor que o investidor decidiu excluir apenas os "voos" mas compridos e definiu que X=100. Se a cotação não voltar ao valor inicial em 100 dias (cerca de três meses), o investidor vende a ação. Como já sabemos do problema dos bêbados, é muito provável que o lucro seja cerca de 10 mil dólares (as cotações estarão abaixo do valor inicial em $10, e são 1.000 as unidades). A probabilidade deste evento é de 1/10. Nos outros 9 casos o investidor recebe o lucro de $1.000 por acordo.

Acontece que os lucros são quase iguais às perdas, então o jogo não vale a pena. Teremos os mesmos problemas com quaisquer X grandes, quando a parte dos voos demasiado longos (voos de Lévy) é proporcional ao quadrado do X. Talvez o jogo seja mais lucrativo com um X menor, quando a lei de potências não funciona?

Obviamente, é impossível ter X=1, pois neste caso - em metade dos casos - as ações serão vendidas com lucro de $1.000 e a outra metade com perda do mesmo valor. Com X=3 haverá ⅝ de acordos lucrativos e ⅜ não lucrativos. O lucro dos acordos lucrativos será igual a $1.000. Dois terços dos acordos não lucrativos terão uma perda de $1.000, e um terço — $3.000. O ganho médio é igual a $(5*1.000−2*1.000−1*3.000)/8=$0. O mesmo acontece com qualquer X.

Depois de ler a seção anterior um trader ativo pode dizer: talvez seja errado limitar o tempo do "passeio aleatório" da cotação quando se pode limitar as perdas. Ou seja, colocar a ordem stop loss - que vende as ações cujo preço desceu - abaixo do valor inicial em M dólares. Mas as leis de potências de distribuição são traiçoeiras, e esta limitação no nosso problema não nos trará lucro.

Se M = -1, então não será lucrativo vender um em cada dois pacotes de ações — não nos parece bem. Com M = -2, a situação fica mais complicada. Com a probabilidade de ½, o investidor terá lucro de $1.000 logo no primeiro dia, mas com a probabilidade de ¼ terá lucro de $2.000 no segundo dia. Com a probabilidade de ⅛ vai ganhar $1.000 no primeiro dia, mas com a probabilidade de 1/16 vai perder $2.000 no quarto dia. Por mais que continuemos estas contas, um lucro médio será sempre igual a 0. E irá passar-se o mesmo com outros valores de M. A perda é sempre proporcional a M e a probabilidade da perda é inversamente proporcional a M. Resultado final: a perda média é igual ao lucro médio.

Vamos fazer uma última tentativa para encontrar uma tática lucrativa neste jogo estranho. Pode-se acreditar que com o jogo eterno o lucro médio seja igual a zero. Torna-se ainda mais claro porque é que um jogo com "cortes" de voos com perdas óbvias também não é lucrativo. Mas porque não fazer, por exemplo, um certo número de acordos por um certo período de tempo? Por exemplo: 10–100 acordos ao longo do período de vida do investidor (digamos 100 anos). Não vamos "não cortar" voos das cotações, mas sim esperar o que for necessário.

Um intervalo de 100 anos deve ser o suficiente para a maioria dos acordos. Por exemplo, se houver 10 acordos, a probabilidade de que pelo menos um dure mais de 100 anos é cerca de 10 raízes de 1/36500, ou seja 1/20. Se houver 100 acordos, esta probabilidade será igual a ½. Há uma probabilidade diferente de zero (e muito grande) de que o investidor terá tempo para fazer alguns acordos. E todos com lucro positivo.

Mas o nosso raciocínio tem um erro. Não vimos o que acontecerá se durante a sua vida o investidor não tiver tempo para fechar as posições. Na verdade isto significa que irá deixar um acordo prolongado a alguém. De facto, uma dívida. E se calcularmos tudo com cuidado, a provável dimensão desta dívida será a mesma que o investidor teve tempo de ganhar - assim como no caso em que "cortámos" um retorno demorado.

Então, as nossas tentativas para encontrar uma tática sempre lucrativa neste jogo lembram a procura de um "movimento perpétuo" — uma tentativa para enganar o simples facto de as oscilações das cotações serem absolutamente aleatórias e os movimentos para cima e para baixo terem uma probabilidade igual. É um jogo típico com resultado zero.

Agora temos de colocar a seguinte questão: o que é que todo este discurso tem a ver com a realidade? O problema dos bêbados era divertido e tinha muitas simplificações. Quando falamos das cotações, surge o funcionamento do mundo financeiro real - o funcionamento da produção, da distribuição de riquezas, etc. Se o mercado funcionasse como um gerador de números aleatórios, não faria sentido jogar com oscilações de preços. Os traders bem-sucedidos poderiam nem existir. Todos os traders não seriam mais que simples jogadores de casino.

Mas a vida real não é matemática ideal - nem casino. Eis algumas diferenças:

Alguns destes fatores (dividendos, ciclos, dependência do mercado e da política) facilitam a vida dos traders. Mas outros (comissões, falência de empresas), pelo contrário, dificultam-na.

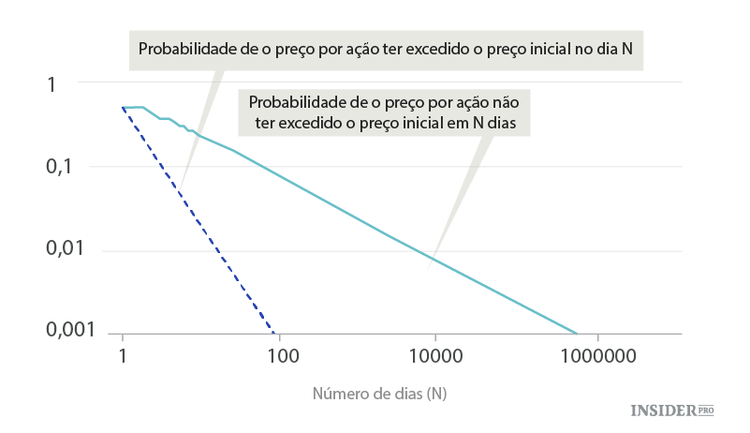
O maior problema é um facto que não existe só em modelos idealizados mas também no comércio real — uma estatística gradual dos tempos de recuperação dos preços (e voos de Lévy). As oscilações no mercado real de ações não são muito aleatórias, mas se acompanharmos várias vezes o tempo de recuperação das cotações, vamos obter gráficos que parecem duas retas em escala logarítmica dupla. De facto, as cotações recuperam, muitas vezes, dentro de um curto espaço de tempo. Mas se não recuperarem por muito tempo, pode ignorá-las.

Devido aos rápidos ciclos diários o preço das ações pode recuperar várias vezes dentro de um dia. Os assim chamados scalpers (cambistas) desfrutam desta situação com bastante frequência: por exemplo, compram uma ação por $50 que dentro de um segundo cai para $49,99 e logo sobe para $50,01. Os scalpers vendem-na e recebem lucro. O scalping lucrativo é possível graças a oscilações aleatórias incompletas e à presença de ciclos.

Mas é necessário lembrar-se da probabilidade dos grandes voos de Lévy. Se um scalper não vir que o preço por ação caiu $1 (100 vezes mais do que pensava), não é razoável achar que o preço vá recuperar dentro de 100 segundos. Se a tendência for positiva, o preço irá recuperar em 10 mil segundos, e se for negativa, pode manter-se baixo por décadas ou séculos. Para um trader que quer ganhar dinheiro agora mesmo, isto não é muito diferente do tempo de recuperação eterno.

Não só num problema idealizado, mas também no mercado de ações real, o preço que se afastou muito da sua posição inicial pode oscilar por um tempo indefinido. Nada o "arrasta" para trás. Se falarmos usando termos matemáticos, o ponto inicial não tem um atractor que seja melhor que os outros. Há probabilidade de que a cotação demore muito a recuperar. E se num passeio aleatório ideal esta probabilidade é incrivelmente pequena, no mundo real a probabilidade não é infinita pois, por exemplo, a empresa pode ir à falência.