Paradoxo da lotaria de São Petersburgo

No âmbito do projeto especial em colaboração com a Corretora Prime EXANTE o Insider.pro continua a série de artigos de divulgação científica "Matemática do Infinito e a Realidade das Finanças" do doutorado em Física e Matemática Viktor Argonov sobre os paradoxos da teoria dos jogos e da sua aplicação a assuntos financeiros. Desta vez relatamos um problema que não se relaciona diretamente com o problema do passeio aleatório - mas que também é incrivelmente paradoxal.

São sugeridas as seguintes regras a um jogador no casino: no início o jogador paga ao casino M dólares (taxa de entrada). Depois o croupier atira uma moeda. Se sair cara, o jogador ganha $1. Se na segunda vez sair cara novamente, o jogador ganha $2. Se saírem três caras seguidas, recebe $4; se quatro caras, $8. E assim por diante, de forma exponencial. Assim que sair coroa, o jogo acaba. O casino leva os M dólares e o jogador fica com aquilo que ganhou.

Colocamos a seguinte questão:

Lucrativo significa que o jogador irá receber mais do que aquilo que pagou inicialmente. Ou seja, irá receber mais do que M.

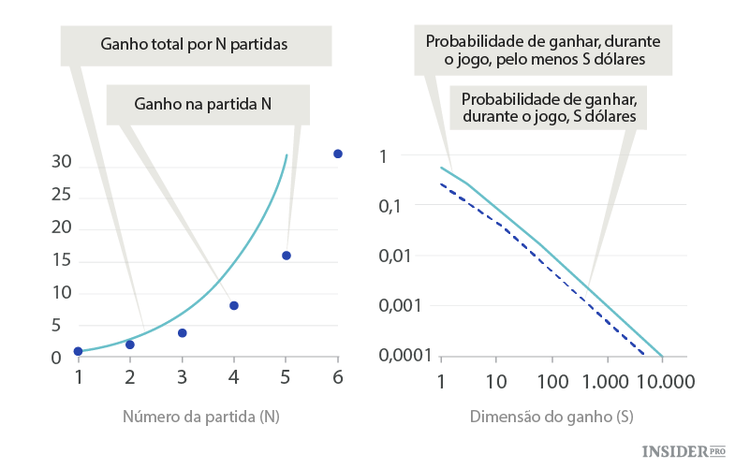
Os gráficos mostram como o lucro cresce com cada passo e qual a probabilidade de ganhar determinada quantia durante o jogo (sem considerar o número M).

O gráfico à esquerda é apresentado de forma linear. Vê-se o quão rapidamente cresce o lucro à medida que o jogo continua. No entanto, a probabilidade de chegar à partida número N diminui à mesma velocidade. Com a primeira partida, o lucro total é igual a $1 e a probabilidade de ficar no jogo nesse momento é ainda de ½. Mas na segunda partida o lucro total é igual a $3 e a probabilidade do jogo continuar é igual a ¼. Na terceira partida o lucro e a probabilidade são de $7 e ⅛, respetivamente. Na quarta partida — $15 e 1/16.

Com um N grande a probabilidade de ficar no jogo é inversamente proporcional ao lucro total. Por exemplo, com a probabilidade de 1/1000 o jogador pode ganhar pelo menos $999.

Os gráficos que mostram a relação entre a probabilidade de lucro e a dimensão do mesmo são apresentados na escala logarítmica à direita. Assim como nos problemas anteriores, surgem como linhas retas (função de potência). Tal significa que será de esperar, novamente, o truque da eternidade.

Vamos supor que a taxa de entrada (M) é de apenas $1. O jogador decide jogar 100 partidas. De acordo com os gráficos irá provavelmente ganhar, pelo menos numa das partidas, $100, compensando as perdas. Numa em cada dez partidas (ou seja, aproximadamente em 10 partidas) o lucro pode ser de $10, o que no total proporciona $100. Quase em metade das partidas restantes os lucros serão pelo menos de $1. O jogo torna-se realmente lucrativo: o jogador abate quase sempre a taxa de entrada e continua com um lucro de $100-300. Se jogar 1000 partidas o lucro será de milhares de dólares.

No entanto, quando a administração do casino perceber que o jogador está a ganhar demasiado, a taxa de entrada subirá de $1 para $10. Será que vale a pena o jogador continuar o jogo?

Agora é que o jogo não parece tão lucrativo. Por exemplo, se o jogador jogar 100 partidas, as perdas serão de $1.000, com ganhos mais ou menos garantidos de $100-300. Trata-se, no entanto, de uma estimativa aproximada. Será possível avaliar os ganhos mais precisamente? Qual será o seu valor médio com um número de partidas ilimitado? Como mostram as fórmulas (mais especificamente, a potencial dependência da probabilidade de ganhar em relação à quantidade ganha), uma característica especial desta lotaria é que os ganhos médios são... Infinitos. Assim, seja qual for o valor de M o jogo será, em média, lucrativo para o jogador.

Depois dos artigos anteriores este facto já não nos surpreende. De facto, no problema da falência do jogador o jogo também era lucrativo com qualquer taxa de entrada. No entanto, o principal paradoxo da LSPB não é a presença da eternidade mas sim a reação psicológica dos jogadores.

À primeira vista, o problema da falência do jogador e o da LSPB apresenta duas conclusões:

Contudo, na prática, a situação é bem diferente. O jogo em que o jogador se alimenta por conta do casino, enquanto este tenta deixá-lo sem dinheiro, é um jogo imaginário. Os casinos reais não costumam realizar jogos tão desfavoráveis para os mesmos (a não ser que seja uma promoção). Mas a LSPB é um jogo que existe na realidade. Os jogadores individuais, e as casas de jogo, organizam este tipo de lotarias e não as consideram um jogo unilateral. A taxa de entrada também importa: poucas pessoas concordam em jogar com um valor de 20 dólares. Porquê?

Nos artigos anteriores mostrámos o quão prudentes devemos ser em relação às soluções que contêm eternidades. Notámos que na realidade a situação pode ser muito pior. O mercado pune regularmente as pessoas que ignoram previsões matemáticas "paradoxais" e os traders sabem disso. Mas no caso da LSPB, a situação pode ser diferente. As previsões matemáticas eternas não importam nesta lotaria - e os desastres financeiros não acontecem. É nisto que consiste o paradoxo de São Petersburgo (PSPB).

O PSPB apresenta várias explicações que podem ser divididas em dois grupos: técnicas e fundamentais. As explicações técnicas fazem um apelo às imperfeições do mundo real em comparação com os modelos matemáticos, e as explicações fundamentais levantam debates filosóficos sobre o fenómeno da mente e do sentido da vida de um ser consciente.

Este grupo de explicações é muito claro. É possível inventar diversas explicações deste tipo - mas relacionam-se todas com as dificuldades técnicas de aplicar a LSPB de forma completa.

Em primeiro lugar, para obter um grande lucro com uma grande probabilidade é melhor não arriscar - mas sim jogar muitas partidas. Quanto maior for a taxa de entrada, mais partidas serão necessárias. Se a taxa de entrada for de $1 (e os ganhos começarem a partir de $1), são necessárias 20 partidas para garantir vantagem. No entanto, com uma taxa de entrada de $10 (com o mesmo ganho de $1) o número de partidas necessárias pode ser tão grande que o casino poderá não permitir - ou então o jogador perderá tanto tempo que o jogo não valerá a pena.

Em segundo lugar, as regras comuns aplicam-se com condições secretas. Se alguém ganhar um milhão por “acidente” o casino pode recusar-se a efetuar o pagamento, justificando-se com falta de dinheiro. Além disso, o casino pode proteger-se de "acidentes" desagradáveis.

Em terceiro lugar, as pessoas disponibilizam-se psicologicamente para ignorar probabilidades pequenas - encarando assim a probabilidade de ganhar mil milhões de dólares, mesmo que a perda máxima possível (quase garantida) seja de pelo menos $500.

No entanto, todas estas explicações não são satisfatórias pois é possível, pelo menos, imaginar uma situação em que todos estes problemas são resolvidos. Porém, mesmo a pessoa mais inteligente e razoável não quer comportar-se "racionalmente".

Para mostrar a imperfeição das explicações técnicas do PSPB, vamos deixar de lado as regras iniciais da lotaria - trocando-as por regras mais simples e rígidas.

Você vai ao casino para um jogo muito simples: numa caixa fechada estão 100 fichas: 99 vermelhas e uma verde. Você pode tirar uma ficha aleatória. Se você tirar uma ficha vermelha, perderá todos os seus haveres. Se tirar a ficha verde, ganhará mil milhões de dólares. Vamos supor que você é uma pessoa comum, da classe média, que tem um apartamento, um carro e eletrodomésticos. Você tem um trabalho comum que permitiu comprar tudo isto ao longo dos anos. Será essa a dimensão da possível perda. Mas o ganho médio (mil milhões de dólares multiplicados pela possibilidade de ganho de 0,01) é de 10 mil milhões de dólares. Vamos supor que o casino está disposto a sofrer perdas (por exemplo, está a realizar o jogo para um programa de televisão) e a pagar o que o jogador ganhar.

Do ponto de vista matemático, o jogo é mais do que lucrativo. Do ponto de vista psicológico, ambos os resultados têm probabilidades bastante significativas. A probabilidade de 1/100 não é tão pequena para ser ignorada. As pessoas muitas vezes compram bilhetes comuns de lotaria com uma probabilidade de ganho muito menor. Mas neste caso é evidente que a maioria das pessoas não vai querer jogar. Exceto marginais (que não têm nada a perder) ou aventureiros patológicos.

Este exemplo prova que não apenas a LSPB, mas também algum outro jogo transparente com dois resultados possíveis e um ganho médio gigante, não garante um comportamento "racional" por parte das pessoas. As condições do jogo parecem inaceitáveis. Porquê?

Todo este raciocínio leva-nos a dois possíveis cenários. Ou a maioria das pessoas pode ser considerada tola (resolvendo incorretamente um problema muito simples) ou é necessário admitir que o comportamento racional não é a mesma coisa que a maximização de lucro e que o verdadeiro bem-estar das pessoas não é proporcional à sua riqueza. A segunda explicação é a correta.

Pesquisas mostram que uma pessoa com um lucro de mil milhões de dólares não pode ser considerada milhões de vezes mais feliz que uma pessoa com um lucro de mil dólares. Psicologicamente, um jogo com uma aposta demasiado alta tem um ganho médio negativo. Para a maioria das pessoas, o lucro de mil milhões de dólares e a perda de todos os seus ativos são comparáveis em termos de gravidade. E já que a probabilidade de ganho é muito menor que a probabilidade de perda, o jogo está fora de questão. Falaremos disso mais detalhadamente no próximo capítulo.